Gradient flow in Laplace Neural Network

In the previous post, I promised to show how the Laplace Neuron might be the key to solving the vanishing and exploding gradient problem. But before we go there, we need to set the stage by building the full network made out of Laplace neurons. Let’s call it the Laplace Neural Network.

I’ll focus on a simple setup: a fully connected network with a single input node, two hidden layers, each with 3 Laplace neurons, and one neuron in the output layer. Nothing too deep, just enough to capture the dynamics.

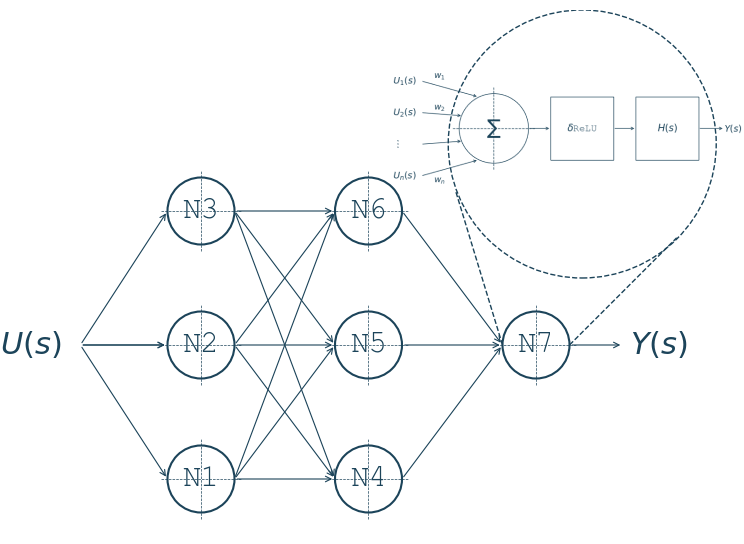
Now, unlike the classical artificial neuron, which is really just a static linear mapping followed by a nonlinearity, the Laplace neuron comes with more moving components. It has memory, delay, and time dynamics, all packed into a single unit. Which means more parameters to tune. But that also means more expressive power, and potentially a much better fit to the systems we’re trying to model.

Let’s revisit the equation of the Laplace Neuron:

Y(s) = \mathcal{L} \left[ \delta\mathrm{ReLU} \left( \mathcal{L}^{-1} \left( \sum_{j=1}^{n} w_j \, U_j(s) \right) \right) \right] \cdot e^{-\theta s} \cdot \frac{K}{\tau s + 1}

We can simplify things a bit. The gain term $K$ can be incorporated into the weights $w_j$, so we don’t need to learn it separately. That leaves us with three key components: the weights $w_j$, the delay $\theta$, and the time constant $\tau$.

To optimize these, we’ll use good old backpropagation. But we're not operating in time. We're doing it in the Laplace domain.

Backpropagation in Laplace domain

Here’s the forward pass of the Laplace neural network we’ll be using as our example:

Z_1(s) = N_1(s) \cdot (w_{U1}U(s) + b_1) $$ $$ Z_2(s) = N_2(s) \cdot (w_{U2}U(s) + b_2) $$ $$ Z_3(s) = N_3(s) \cdot (w_{U3}U(s) + b_3) $$ $$ Z_4(s) = N_4(s) \cdot (w_{14}Z_1(s) + w_{24}Z_2(s) + w_{34}Z_3(s) + b_4) $$ $$ Z_5(s) = N_5(s) \cdot (w_{15}Z_1(s) + w_{25}Z_2(s) + w_{35}Z_3(s) + b_5) $$ $$ Z_6(s) = N_6(s) \cdot (w_{16}Z_1(s) + w_{26}Z_2(s) + w_{36}Z_3(s) + b_6) $$ $$ Y(s) = N_7(s) \cdot (w_{47}Z_4(s) + w_{57}Z_5(s) + w_{67}Z_6(s) + b_7)

where:

$Y(s)$ is the output of the network
$N_j(s)$ is the function representing the $j$-th Laplace Neuron
$Z_j(s)$ is the output signal from the $j$-th neuron
$w_{pq}$ is the weight parameter of the connection from neuron $N_p$ to neuron $N_q$
$b_j$ is the bias parameter of the $j$-th neuron

Now, let's explore how to backpropagate the error, not through time, but through the structure of the network in the $s$ (Laplace) domain.

We’ve got an output signal from the Laplace neural network, and now it’s time to see how well it holds up against reality. So we compare it to the measured, or let’s say, the true signal. That comparison gives us an error, a measure of how close (or far) our generated output is from what actually happens out there in the world. That error also tells us in which direction we need to adjust the system’s parameters to get closer to the desired result.

Now the goal is simple: tweak the network parameters so that this error shrinks, as close to zero as we can get it. Every parameter, every weight, every internal constant in every Laplace neuron must be updated in the right direction.

And we’ll do that the by writing out the partial derivatives, one by one, tracing how the error flows through the network, from the output all the way back to the input.

This time, though, the path of the gradient isn’t traced through a static feedforward map, it’s traced through time-evolving, memory-bearing dynamical systems.

Let’s start writing down the update rule of weights and biases:

\frac{\partial error}{\partial w_{67}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial w_{67}} = \frac{\partial error}{\partial Y(s)} \cdot N_7(s) \cdot Z_{6}(s) $$ $$ \frac{\partial error}{\partial w_{57}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial w_{57}} = \frac{\partial error}{\partial Y(s)} \cdot N_7(s) \cdot Z_{5}(s) $$ $$ \frac{\partial error}{\partial w_{47}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial w_{47}} = \frac{\partial error}{\partial Y(s)} \cdot N_7(s) \cdot Z_{4}(s) $$ $$ \frac{\partial error}{\partial w_{36}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial w_{36}} = \frac{\partial error}{\partial Y(s)} \cdot w_{67}N_7(s) \cdot N_6(s) \cdot Z_{3}(s) $$ $$ \frac{\partial error}{\partial w_{26}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial w_{26}} = \frac{\partial error}{\partial Y(s)} \cdot w_{67}N_7(s) \cdot N_6(s) \cdot Z_{2}(s) $$ $$ \frac{\partial error}{\partial w_{16}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial w_{16}} = \frac{\partial error}{\partial Y(s)} \cdot w_{67}N_7(s) \cdot N_6(s) \cdot Z_{1}(s) $$ $$ \frac{\partial error}{\partial w_{35}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial w_{35}} = \frac{\partial error}{\partial Y(s)} \cdot w_{57}N_7(s) \cdot N_5(s) \cdot Z_{3}(s) $$ $$ \frac{\partial error}{\partial w_{25}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial w_{25}} = \frac{\partial error}{\partial Y(s)} \cdot w_{57}N_7(s) \cdot N_5(s) \cdot Z_{2}(s) $$ $$ \frac{\partial error}{\partial w_{15}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial w_{15}} = \frac{\partial error}{\partial Y(s)} \cdot w_{57}N_7(s) \cdot N_5(s) \cdot Z_{1}(s) $$ $$ \frac{\partial error}{\partial w_{34}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial w_{34}} = \frac{\partial error}{\partial Y(s)} \cdot w_{47}N_7(s) \cdot N_4(s) \cdot Z_{3}(s) $$ $$ \frac{\partial error}{\partial w_{24}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial w_{24}} = \frac{\partial error}{\partial Y(s)} \cdot w_{47}N_7(s) \cdot N_4(s) \cdot Z_{2}(s) $$ $$ \frac{\partial error}{\partial w_{14}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial w_{14}} = \frac{\partial error}{\partial Y(s)} \cdot w_{47}N_7(s) \cdot N_4(s) \cdot Z_{1}(s)

\begin{aligned} \frac{\partial error}{\partial w_{U3}} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial w_{U3}} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial w_{U3}} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial w_{U3}} \right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67} N_7(s) \cdot w_{36} N_6(s) \cdot N_3(s) \cdot U(s) + w_{57} N_7(s) \cdot w_{35} N_5(s) \cdot N_3(s) \cdot U(s) + w_{47} N_7(s) \cdot w_{34} N_4(s) \cdot N_3(s) \cdot U(s) \right] \end{aligned} $$ $$ \begin{aligned} \frac{\partial error}{\partial w_{U2}} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial w_{U2}} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial w_{U2}} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial w_{U2}} \right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67} N_7(s) \cdot w_{26} N_6(s) \cdot N_2(s) \cdot U(s) + w_{57} N_7(s) \cdot w_{25} N_5(s) \cdot N_2(s) \cdot U(s) + w_{47} N_7(s) \cdot w_{24} N_4(s) \cdot N_2(s) \cdot U(s) \right] \end{aligned} $$ $$ \begin{aligned} \frac{\partial error}{\partial w_{U1}} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial w_{U1}} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial w_{U1}} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial w_{U1}} \right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67} N_7(s) \cdot w_{16} N_6(s) \cdot N_1(s) \cdot U(s) + w_{57} N_7(s) \cdot w_{15} N_5(s) \cdot N_1(s) \cdot U(s) + w_{47} N_7(s) \cdot w_{14} N_4(s) \cdot N_1(s) \cdot U(s) \right] \end{aligned}

\frac{\partial error}{\partial b_7} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial b_7} = \frac{\partial error}{\partial Y(s)} \cdot N_7(s) $$ $$ \frac{\partial error}{\partial b_{6}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial b_{6}} = \frac{\partial error}{\partial Y(s)} \cdot w_{67} N_7(s) \cdot N_6(s) $$ $$ \frac{\partial error}{\partial b_{5}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial b_{5}} = \frac{\partial error}{\partial Y(s)} \cdot w_{57} N_7(s) \cdot N_5(s) $$ $$ \frac{\partial error}{\partial b_{4}} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial b_{4}} = \frac{\partial error}{\partial Y(s)} \cdot w_{47} N_7(s) \cdot N_4(s)

\begin{aligned} \frac{\partial error}{\partial b_{3}} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial b_{3}} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial b_{3}} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial b_{3}}\right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67}N_7(s) \cdot w_{36}N_6(s) \cdot N_3(s) + w_{57}N_7(s) \cdot w_{35}N_5(s) \cdot N_3(s) + w_{47}N_7(s) \cdot w_{34}N_4(s) \cdot N_3(s) \right] \end{aligned} $$ $$ \begin{aligned} \frac{\partial error}{\partial b_{2}} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial b_{2}} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial b_{2}} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial b_{2}}\right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67}N_7(s) \cdot w_{26}N_6(s) \cdot N_2(s) + w_{57}N_7(s) \cdot w_{25}N_5(s) \cdot N_2(s) + w_{47}N_7(s) \cdot w_{24}N_4(s) \cdot N_2(s) \right] \end{aligned} $$ $$ \begin{aligned} \frac{\partial error}{\partial b_{1}} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial b_{1}} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial b_{1}} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial b_{1}}\right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67}N_7(s) \cdot w_{16}N_6(s) \cdot N_1(s) + w_{57}N_7(s) \cdot w_{15}N_5(s) \cdot N_1(s) + w_{47}N_7(s) \cdot w_{14}N_4(s) \cdot N_1(s) \right] \end{aligned}

And now we'll write down the updating rules of parameters $\tau$ and $\theta$ for every Laplace neuron:

\frac{\partial error}{\partial \tau_7} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial N_7(s)} \cdot \frac{\partial N_7(s)}{\partial \tau_7} = \frac{\partial error}{\partial Y(s)} \cdot (w_{47}Z_{4}(s) + w_{57}Z_{5}(s) + w_{67}Z_{6}(s)) \cdot \frac{\partial N_7(s)}{\partial \tau_7} $$ $$ \frac{\partial error}{\partial \theta_7} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial N_7(s)} \cdot \frac{\partial N_7(s)}{\partial \theta_7} = \frac{\partial error}{\partial Y(s)} \cdot (w_{47}Z_{4}(s) + w_{57}Z_{5}(s) + w_{67}Z_{6}(s)) \cdot \frac{\partial N_7(s)}{\partial \theta_7} $$ $$ \frac{\partial error}{\partial \tau_6} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial N_6(s)} \cdot \frac{\partial N_6(s)}{\partial \tau_6} = \frac{\partial error}{\partial Y(s)} \cdot w_{67} N_7(s) \cdot (w_{16}Z_{1}(s) + w_{26}Z_{2}(s) + w_{36}Z_{3}(s)) \cdot \frac{\partial N_6(s)}{\partial \tau_6} $$ $$ \frac{\partial error}{\partial \theta_6} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial N_6(s)} \cdot \frac{\partial N_6(s)}{\partial \theta_6} = \frac{\partial error}{\partial Y(s)} \cdot w_{67} N_7(s) \cdot (w_{16}Z_{1}(s) + w_{26}Z_{2}(s) + w_{36}Z_{3}(s)) \cdot \frac{\partial N_6(s)}{\partial \theta_6} $$ $$ \frac{\partial error}{\partial \tau_5} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial N_5(s)} \cdot \frac{\partial N_5(s)}{\partial \tau_5} = \frac{\partial error}{\partial Y(s)} \cdot w_{57} N_7(s) \cdot (w_{15}Z_{1}(s) + w_{25}Z_{2}(s) + w_{35}Z_{3}(s)) \cdot \frac{\partial N_5(s)}{\partial \tau_5} $$ $$ \frac{\partial error}{\partial \theta_5} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial N_5(s)} \cdot \frac{\partial N_5(s)}{\partial \theta_5} = \frac{\partial error}{\partial Y(s)} \cdot w_{57} N_7(s) \cdot (w_{15}Z_{1}(s) + w_{25}Z_{2}(s) + w_{35}Z_{3}(s)) \cdot \frac{\partial N_5(s)}{\partial \theta_5} $$ $$ \frac{\partial error}{\partial \tau_4} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial N_4(s)} \cdot \frac{\partial N_4(s)}{\partial \tau_4} = \frac{\partial error}{\partial Y(s)} \cdot w_{47} N_7(s) \cdot (w_{14}Z_{1}(s) + w_{24}Z_{2}(s) + w_{34}Z_{3}(s)) \cdot \frac{\partial N_4(s)}{\partial \tau_4} $$ $$ \frac{\partial error}{\partial \theta_4} = \frac{\partial error}{\partial Y(s)} \cdot \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial N_4(s)} \cdot \frac{\partial N_4(s)}{\partial \theta_4} = \frac{\partial error}{\partial Y(s)} \cdot w_{47} N_7(s) \cdot (w_{14}Z_{1}(s) + w_{24}Z_{2}(s) + w_{34}Z_{3}(s)) \cdot \frac{\partial N_4(s)}{\partial \theta_4}

\begin{aligned} \frac{\partial error}{\partial \tau_3} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial N_3(s)} \cdot \frac{\partial N_3(s)}{\partial \tau_3} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial N_3(s)} \cdot \frac{\partial N_3(s)}{\partial \tau_3} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial N_3(s)} \cdot \frac{\partial N_3(s)}{\partial \tau_3}\right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67} N_7(s) \cdot w_{36} N_6(s) \cdot w_{U3} U(s) \cdot \frac{\partial N_3(s)}{\partial \tau_3} + w_{57} N_7(s) \cdot w_{35} N_5(s) \cdot w_{U3} U(s) \cdot \frac{\partial N_3(s)}{\partial \tau_3} + w_{47} N_7(s) \cdot w_{34} N_4(s) \cdot w_{U3} U(s) \cdot \frac{\partial N_3(s)}{\partial \tau_3}\right] \end{aligned} $$ $$ \begin{aligned} \frac{\partial error}{\partial \theta_3} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial N_3(s)} \cdot \frac{\partial N_3(s)}{\partial \theta_3} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial N_3(s)} \cdot \frac{\partial N_3(s)}{\partial \theta_3} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{3}(s)} \cdot \frac{\partial Z_{3}(s)}{\partial N_3(s)} \cdot \frac{\partial N_3(s)}{\partial \theta_3}\right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67} N_7(s) \cdot w_{36} N_6(s) \cdot w_{U3} U(s) \cdot \frac{\partial N_3(s)}{\partial \theta_3} + w_{57} N_7(s) \cdot w_{35} N_5(s) \cdot w_{U3} U(s) \cdot \frac{\partial N_3(s)}{\partial \theta_3} + w_{47} N_7(s) \cdot w_{34} N_4(s) \cdot w_{U3} U(s) \cdot \frac{\partial N_3(s)}{\partial \theta_3}\right] \end{aligned} $$ $$ \begin{aligned} \frac{\partial error}{\partial \tau_2} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial N_2(s)} \cdot \frac{\partial N_2(s)}{\partial \tau_2} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial N_2(s)} \cdot \frac{\partial N_2(s)}{\partial \tau_2} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial N_2(s)} \cdot \frac{\partial N_2(s)}{\partial \tau_2}\right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67} N_7(s) \cdot w_{26} N_6(s) \cdot w_{U2} U(s) \cdot \frac{\partial N_2(s)}{\partial \tau_2} + w_{57} N_7(s) \cdot w_{25} N_5(s) \cdot w_{U2} U(s) \cdot \frac{\partial N_2(s)}{\partial \tau_2} + w_{47} N_7(s) \cdot w_{24} N_4(s) \cdot w_{U2} U(s) \cdot \frac{\partial N_2(s)}{\partial \tau_2}\right] \end{aligned} $$ $$ \begin{aligned} \frac{\partial error}{\partial \theta_2} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial N_2(s)} \cdot \frac{\partial N_2(s)}{\partial \theta_2} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial N_2(s)} \cdot \frac{\partial N_2(s)}{\partial \theta_2} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{2}(s)} \cdot \frac{\partial Z_{2}(s)}{\partial N_2(s)} \cdot \frac{\partial N_2(s)}{\partial \theta_2}\right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67} N_7(s) \cdot w_{26} N_6(s) \cdot w_{U2} U(s) \cdot \frac{\partial N_2(s)}{\partial \theta_2} + w_{57} N_7(s) \cdot w_{25} N_5(s) \cdot w_{U2} U(s) \cdot \frac{\partial N_2(s)}{\partial \theta_2} + w_{47} N_7(s) \cdot w_{24} N_4(s) \cdot w_{U2} U(s) \cdot \frac{\partial N_2(s)}{\partial \theta_2}\right] \end{aligned} $$ $$ \begin{aligned} \frac{\partial error}{\partial \tau_1} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial N_1(s)} \cdot \frac{\partial N_1(s)}{\partial \tau_1} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial N_1(s)} \cdot \frac{\partial N_1(s)}{\partial \tau_1} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial N_1(s)} \cdot \frac{\partial N_1(s)}{\partial \tau_1}\right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67} N_7(s) \cdot w_{16} N_6(s) \cdot w_{U1} U(s) \cdot \frac{\partial N_1(s)}{\partial \tau_1} + w_{57} N_7(s) \cdot w_{15} N_5(s) \cdot w_{U1} U(s) \cdot \frac{\partial N_1(s)}{\partial \tau_1} + w_{47} N_7(s) \cdot w_{14} N_4(s) \cdot w_{U1} U(s) \cdot \frac{\partial N_1(s)}{\partial \tau_1}\right] \end{aligned} $$ $$ \begin{aligned} \frac{\partial error}{\partial \theta_1} &= \frac{\partial error}{\partial Y(s)} \cdot \left[ \frac{\partial Y(s)}{\partial Z_{6}(s)} \cdot \frac{\partial Z_{6}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial N_1(s)} \cdot \frac{\partial N_1(s)}{\partial \theta_1} + \frac{\partial Y(s)}{\partial Z_{5}(s)} \cdot \frac{\partial Z_{5}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial N_1(s)} \cdot \frac{\partial N_1(s)}{\partial \theta_1} + \frac{\partial Y(s)}{\partial Z_{4}(s)} \cdot \frac{\partial Z_{4}(s)}{\partial Z_{1}(s)} \cdot \frac{\partial Z_{1}(s)}{\partial N_1(s)} \cdot \frac{\partial N_1(s)}{\partial \theta_1}\right] \\ &= \frac{\partial error}{\partial Y(s)} \cdot \left[ w_{67} N_7(s) \cdot w_{16} N_6(s) \cdot w_{U1} U(s) \cdot \frac{\partial N_1(s)}{\partial \theta_1} + w_{57} N_7(s) \cdot w_{15} N_5(s) \cdot w_{U1} U(s) \cdot \frac{\partial N_1(s)}{\partial \theta_1} + w_{47} N_7(s) \cdot w_{14} N_4(s) \cdot w_{U1} U(s) \cdot \frac{\partial N_1(s)}{\partial \theta_1}\right] \end{aligned}

This might look a bit intimidating at first glance, but it’s not as bad as it seems. A lot of structure hides in these equations. There are patterns, and once you spot them, the whole thing starts to simplify. That said, a careful reader might notice that we’re not quite done yet. To properly update our parameters, we still need to say what $\frac{\partial N(s)}{\partial \tau}$ and $\frac{\partial N(s)}{\partial \theta}$ actually mean. So let’s do that.

Remember, $N(s)$ is a function that represents the behavior of a Laplace neuron receiving weighted inputs and firing after threshold is reached.

Now, to adjust the internal parameters $\tau$ and $\theta$, we need to partially differentiate this function. In other words, we have to unpack what $N$ is doing with respect to each of these values, so we can know exactly how a change in one affects the overall output.

Let’s write it out:

\frac{\partial N(s)}{\partial \tau} = \frac{\partial \left( \mathcal{L} \left\{ \delta\mathrm{ReLU} \left[ \mathcal{L}^{-1} \left( \sum_{j=1}^{n} w_j \, U_j(s) \right) \right] \right\} \cdot e^{-\theta s} \frac{1}{\tau s + 1}\right)}{\partial \tau} = \mathcal{L} \left\{ \delta\mathrm{ReLU} \left[ \mathcal{L}^{-1} \left( \sum_{j=1}^{n} w_j \, U_j(s) \right) \right] \right\} \cdot e^{-\theta s} \frac{-s}{(\tau s + 1)^2} $$ $$ \frac{\partial N(s)}{\partial \theta} = \frac{\partial \left( \mathcal{L} \left\{ \delta\mathrm{ReLU} \left[ \mathcal{L}^{-1} \left( \sum_{j=1}^{n} w_j \, U_j(s) \right) \right] \right\} \cdot e^{-\theta s} \frac{1}{\tau s + 1} \right)}{\partial \theta} = \mathcal{L} \left\{ \delta\mathrm{ReLU} \left[ \mathcal{L}^{-1} \left( \sum_{j=1}^{n} w_j \, U_j(s) \right) \right] \right\} \cdot e^{-\theta s} \frac{-s}{\tau s + 1}

We can also write out the partial derivative of the $\delta$ReLU, just to get some intuition about what happens to the derivative when the threshold is reached:

\frac{\partial N(s)}{\partial \delta \mathrm{ReLU}} = \frac{\partial \left( \mathcal{L} \left\{ \delta\mathrm{ReLU} \left[ \mathcal{L}^{-1} \left( \sum_{j=1}^{n} w_j \, U_j(s) \right) \right] \right\} \cdot e^{-\theta s} \frac{1}{\tau s + 1}\right)}{\partial \delta \mathrm{ReLU}} = \begin{cases} (\sum_{\atop{j=1}}^{n} {w_j}{ U_j(s)) \cdot e^{-\theta s}\frac{1}{\tau s+1}}) & \text{if } x>\delta \\ 0 & \text{otherwise} \end{cases}

which means, if the threshold isn’t reached, there will be no gradient flow through that branch during backpropagation. And that makes sense since that branch didn’t contribute to the final error, it shouldn’t be part of the update.

Stability

So how to maintain the training process stable?

We definitely don’t want our network suddenly returning out NaN or Inf values mid-training. That’s usually a sign that something went off the rails, literally. Fortunately, there’s a simple trick we can borrow from Control Theory.

In control systems, the stability of a linear system is determined by the location of its poles.

So what are poles?

Let’s write the transfer function in the standard form:

$$ H(s) = \frac{num(s)}{den(s)} $$

Poles are defined as the roots of the denominator polynomial of the transfer function, where $den(s) = 0$. In our example the transfer function has:

$$ den(s) = \tau s + 1 $$

which means we get a single pole at:

$$ s = -\frac{1}{\tau} $$

Now, here’s the key insight: the position of that pole in the complex plane tells us whether a system is stable, unstable or marginally stable.

If the pole lies in the open left-half of the complex plane, the system is stable.
If any pole crosses into the right-half, the system becomes unstable.
And if a pole lands right on the imaginary axis (real part is zero), the system is marginally stable. It might oscillate forever without settling.

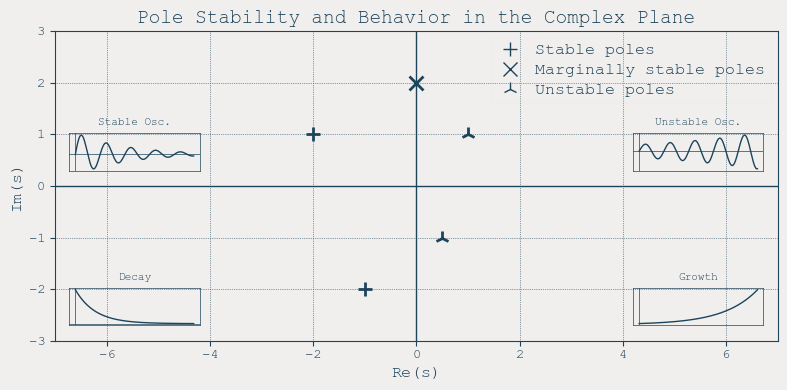
So what does this mean for our training process? Well, to keep its dynamics stable, we need to make sure that the pole stays on the left side. In our case, that simply means keeping $\tau > 0$ If $\tau$ becomes zero or negative during training, the pole jumps into the unstable zone, and things start exploding numerically.

To prevent that, we can apply a simple constraint during training: clip the gradient so that $\tau$ never drops below a small positive value. Something like $\tau > \epsilon$, where $\epsilon$ is an infinitesimally small number, just enough to keep things on the safe side of the plane.

If every neuron in the network maintains this constraint, if every little system stays stable, the whole network remains stable too.

Now that we’ve shown how the Laplace Neural Network updates its parameters in the Laplace domain, it’s time to test it on some simple examples and compare its performance to an RNN of the same complexity.

Stay tuned for the next post, where we’ll see how the Laplace Neural Network stacks up against the RNN on a basic linear dynamical system and whether it can extrapolate outside the training distribution effectively.

It gets interesting.

Gradient flow in Laplace Neural Network

Backpropagation in Laplace domain

Stability

References: